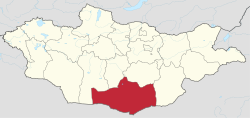
Ömnögovi Province
Ömnögovi Province
Өмнөговь аймаг ᠡᠮᠦᠨᠡᠭᠣᠪᠢᠠᠶᠢᠮᠠᠭ | |
|---|---|
 Landscape in Ömnögovi Province | |
 | |
| Coordinates: 43°0′N 104°15′E / 43.000°N 104.250°E | |
| Country | Mongolia |
| Established | 1931 |
| Capital | Dalanzadgad |
| Area | |
| • Total | 165,380.47 km2 (63,853.76 sq mi) |
| Population (2023) | |
| • Total | 76,153 |
| • Density | 0.46/km2 (1.2/sq mi) |
| GDP | |
| • Total | MNT 3,429 billion US$ 1.0 billion (2023) |
| • Per capita | MNT 45,028,216 US$ 13,202 (2023) |
| Time zone | UTC+8 |
| Area code | +976 (0)153 |
| ISO 3166 code | MN-053 |
| Vehicle registration | ӨМ_ |
| Website | www |

Ömnögovi (Mongolian: Өмнөговь Ömnögovǐ, South Gobi) is an aimag (province) of Mongolia, located in the south of the country, in the Gobi Desert. Ömnögovi is Mongolia's largest aimag. The capital is Dalanzadgad.
The province is rich in mineral deposits, including gold and copper. Agriculture is of minor importance. Vegetables are grown in some oases -for example, in Dal near Dalanzadgad.
As the aimag has various sights to offer, tourism is gaining importance. Ömnögovi includes several well known tourist areas, including the Flaming Cliffs, Gobi Gurvansaikhan National Park and Khongoryn Els - The Singing Sand Dunes.
Transportation
[edit]The Dalanzadgad Airport (ZMDZ/DLZ) has one concrete runway. It is served by regular domestic flights from and to Ulaanbaatar.
Administrative subdivisions
[edit]| Sum | Mongolian | Population (1994)[2] |
Population (2003)[3] |
Population (2005)[4] |
Population (2009)[5] |
Sum centre population |
Area (km2)[3] |
Density (/km2) |
|---|---|---|---|---|---|---|---|---|
| Bayan-Ovoo | Баян-Овоо | 1,577 | 1,569 | 1,539 | 1,574 | 544 | 10,474 | 0.15 |
| Bayandalai | Баяндалай | 2,125 | 2,360 | 2,338 | 2,316 | 651 | 10,751 | 0.22 |
| Bulgan | Булган | 2,421 | 2,433 | 2,430 | 2,395 | 929 | 7,498 | 0.32 |
| Dalanzadgad | Даланзадгад | 12,391 | 15,308 | 15,954 | 17,946 | 16,856 | 476 | 37.70 |
| Gurvan tes | Гурван тэс | 2,983 | 3,376 | 3,524 | 4,034 | 1,842 | 27,967 | 0.14 |
| Khanbogd | Ханбогд | 2,161 | 2,451 | 2,659 | 3,154 | 1,361 | 15,151 | 0.21 |
| Khan khongor | Хан хонгор | 2,559 | 2,931 | 2,542 | 2,376 | 616 | 9,931 | 0.24 |
| Khürmen | Хүрмэн | 1,968 | 1,951 | 1,910 | 1,796 | 495 | 12,393 | 0.14 |
| Mandal-Ovoo | Мандал-Овоо | 2,345 | 2,166 | 2,004 | 1,954 | 603 | 6,433 | 0.30 |
| Manlai | Манлай | 2,215 | 2,422 | 2,431 | 2,450 | 608 | 12,418 | 0.20 |
| Nomgon | Номгон | 2,608 | 3,045 | 3,009 | 2,869 | 787 | 19,468 | 0.15 |
| Noyon | Ноён | 1,417 | 1,468 | 1,390 | 1,318 | 401 | 10,550 | 0.12 |
| Sevrei | Сэврэй | 2,216 | 2,423 | 2,309 | 2,191 | 709 | 8,095 | 0.27 |
| Tsogt-Ovoo | Цогт-Овоо | 1,863 | 1,761 | 1,672 | 1,666 | 619 | 6,526 | 0.26 |
| Tsogttsetsii | Цогтцэций | 1,990 | 2,130 | 2,155 | 2,642 | 1,043 | 7,246 | 0.36 |
-
Landscape in Ömnögovi Aimag
-
A Khulan (Mongolian Wild Ass) on a hill in the Gobi of the Ömnögovi, at sunset.
-
Growing vegetables in oasis Dal.
Religion
[edit]Religion in Ömnögovi (2009)[6]
According to a 2009 survey, 73.5% of the residents of Ömnögovi are Buddhists, 2.9% are Christians, 23.3% do not identify with a formal religion, and 0.3% adhere to other formal religions.[6]
References
[edit]- ^ "GROSS DOMESTIC PRODUCT, by region, aimags and the Capital". www.1212.mn. Mongolian Statistical Information Service. Retrieved 2023-12-06.
- ^ "ANNEX I Timeline : A Brief History of Mongolia" (PDF). Wayback.archive-it.org. Retrieved 5 March 2022.
- ^ a b Statistics office of Ömnögovi Aimag Archived March 26, 2007, at the Wayback Machine
- ^ Official site of Ömnögovi Aimag Archived June 13, 2007, at the Wayback Machine
- ^ "Ömnögovi Aimag Statistical Office". Archived from the original on 21 April 2012. Retrieved 5 March 2022.
- ^ a b Data from Oyu Tolgoi Project. Social, Economic and Environmental Subset, Centre for Policy Research, Population Training and Research Centre, 2009. p. 10, Ifcext.ifc.org
External links
[edit]